RSA | Regnum Artificis

What is RSA

RSA was developed by Ron Rivest, Adi Shamir, and Leonard Adleman in 1977. It is based on the assumption that factoring the product of two large prime numbers is computationally difficult.

RSA Mechanism

1. Key Generation

Choose two large prime numbers $p$ and $q$
Compute $n = p \times q$
Compute Euler’s totient $\phi(n) = (p - 1)(q - 1)$
Choose an integer $e$ such that $ 1 < e < \phi(n)$ and $gcd(e, \phi(n))=1$
Compute $d$ such that $ e \times d \equiv 1 (\mod \phi(n))$.
The Public key is $(e, n)$ and the private key is $(d, n)$.

2. Encryption To encrypt a message $M$: $$ C = M^{e} \mod n $$

3. Decryption To decrypt a ciphertext $C$ $$ M = C^{d} \mod n $$

Vulnerabilities

1. Common Factor Attack

1. Common Factor Attack

In RSA, the modulus $N$ is the product of two large primes.
However, if two different RSA key pairs happen to share a common prime factor—meaning their $N$ values have a nontrivial GCD—the private keys can be efficiently recovered using the Euclidean algorithm.
This vulnerability often occurs when poor entropy is used during key generation. In case of that, It satisfies

$$ gcd(N_{1}, N_{2}) = p $$

so both private keys can be broken. This is a Catastarophic vulnerability that results from weak or reused random number generator during RSA Key Generation.

Example : Is RSA Can be Broken?

Take a look at CTF question at PicoCTF. Our Objective is to crack the ciphertext and get the flag

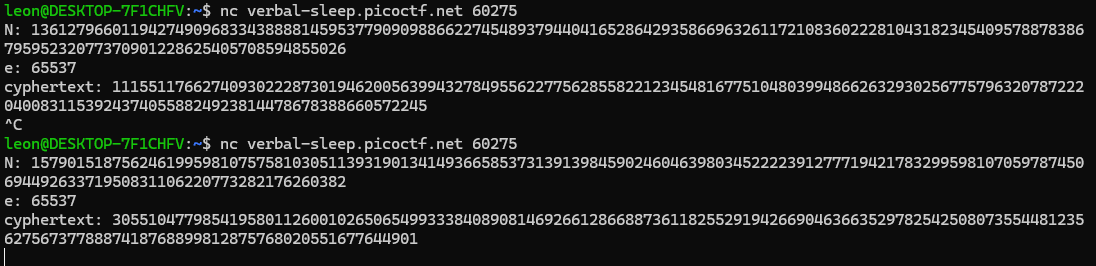
picoCTF question

I execute encryption program by accessing to the verbal-sleep.pico.net with port number 60275 and nc commands on WSL. We know that We have different Ns. But, Let’s take a look at the code that have provided by the organizer.

from sys import exit
from Crypto.Util.number import bytes_to_long, inverse
from setup import get_primes

e = 65537

def gen_key(k):
    """
    Generates RSA key with k bits
    """
    p, q = get_primes(k // 2)
    N = p * q
    d = inverse(e, (p - 1) * (q - 1))

    return ((N, e), d)

def encrypt(pubkey, m):
    N, e = pubkey
    return pow(bytes_to_long(m.encode('utf-8')), e, N)

def main(flag):
    pubkey, _privkey = gen_key(1024)
    encrypted = encrypt(pubkey, flag)
    return (pubkey[0], encrypted)

if __name__ == "__main__":
    flag = open('flag.txt', 'r').read()
    flag = flag.strip()
    N, cypher  = main(flag)
    print("N:", N)
    print("e:", e)
    print("cyphertext:", cypher)
    exit()

You can see the input parameter of gen_key function and it has 1024 as fixed-input. The problem is that both of N can be factorized by GCD(Great Common Divisior) and so can find another prime in the first turn.

The solution is as follows:

First, find the GCD of both N values.
Then, find the other prime factor by dividing N by the GCD.
Compute $\phi(n)$ as $(p - 1)(q - 1)$.
Compute $d$ as the modular inverse of $e$ modulo $\phi(n)$.
Decrypt the ciphertext using $M = C^d \mod n$.
Convert the resulting integer into bytes, then decode it as UTF-8.
Finally, you will get the flag!

Solution Code

Here is the solution code. Originally, I wrote the code in JupyterLab and later adapted it to run as a standalone Python script.

from Crypto.Util.number import inverse, long_to_bytes
import math

# First : Check the GCD of N1, N2 then You can get p.(the gcd of n1, n2 is p)
p = math.gcd(N1, N2)
q = N1 // p

# Calculate phi(N)
phi1 = (p-1) * (q-1)

# Calculate d
d = inverse(e, phi1)

# decrypted msg

decrypted_msg = pow(cipher1, d, N1)

# the value is number, we must convert it into plaintext
long_to_bytes(decrypted_msg).decode('utf-8')

What is RSA#

RSA Mechanism#

Vulnerabilities#

1. Common Factor Attack#

Example : Is RSA Can be Broken?#

Solution Code#